Print Options

Card layout: ?

← Back to notecard set|Easy Notecards home page

Instructions for Side by Side Printing
  1. Print the notecards
  2. Fold each page in half along the solid vertical line
  3. Cut out the notecards by cutting along each horizontal dotted line
  4. Optional: Glue, tape or staple the ends of each notecard together
  1. Verify Front of pages is selected for Viewing and print the front of the notecards
  2. Select Back of pages for Viewing and print the back of the notecards
    NOTE: Since the back of the pages are printed in reverse order (last page is printed first), keep the pages in the same order as they were after Step 1. Also, be sure to feed the pages in the same direction as you did in Step 1.
  3. Cut out the notecards by cutting along each horizontal and vertical dotted line
To print: Ctrl+PPrint as a list

21 notecards = 6 pages (4 cards per page)

Viewing:

CHEM 23: Statistics and Data Handling in Analytical Chemistry

front 1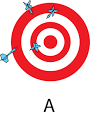

back 1

low accuracy, low precision

front 2

back 2

low accuracy, high precision

front 3

back 3

high accuracy, low preicison

front 4

back 4

high accuracy, high precision

front 5

accuracy

back 5

agreement between a measured value and the accepted true value, how close would it be to the actual value

front 6

ways to express accuracy

back 6

absolute error and relative error

front 7

absolute error formula

back 7

measured value – true value

front 8

relative error formula

back 8

((measured value - true value)/(true value)) x 100%

front 9

precision

back 9

degree of agreement between replicate measurements of the same quantity

front 10

determinate errors

back 10

determinable and that presumably can be either avoided or corrected

front 11

instrumental errors

back 11

faulty equipment

front 12

example of instrumental error

back 12

uncalibrated glassware

front 13

operative errors

back 13

personal errors

front 14

example of operative error

back 14

mathematical error in calculation, misread of menisicus

front 15

errors of the method

back 15

wrong method for an experiment

front 16

example of error of the method

back 16

coprecipitation of impurities

front 17

indeterminate errors

back 17

accidental or random errors

front 18

what does indeterminate error show in a distribution?

back 18

bell curve or normal distribution

front 19

significant figures

back 19

the number of digits necessary to express the results of a measurement consistent with the measured precision

front 20

significant figure rule in addition and subtraction

back 20

use least significant decimal place

front 21

significant figure rule in multiplication and division

back 21

use least significant figures