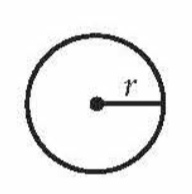
Area of a Circle

πr²

Circumference of a Circle

2πr

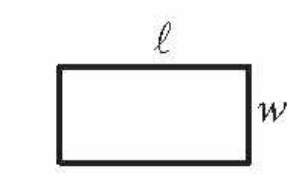
Area of a Rectangle

lw

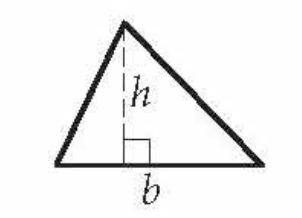
Area of a Triangle

(1/2)bh

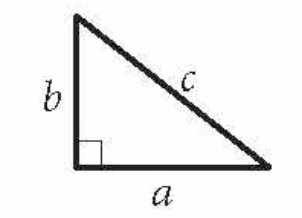
Pythagorean Theorem

c²=a²+b²

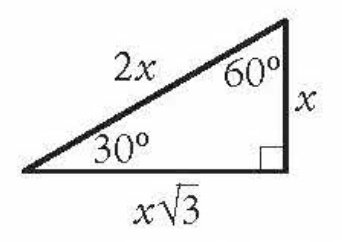
Special Right Triangle

Across from 30 - x

Across from 60 - x√3

Across from 90 - 2x

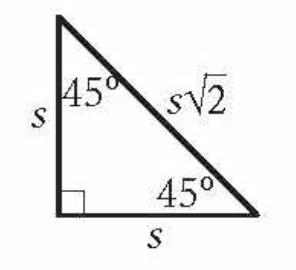
Special Right Triangle

Across from 45 - s

Across from 90 - s√2

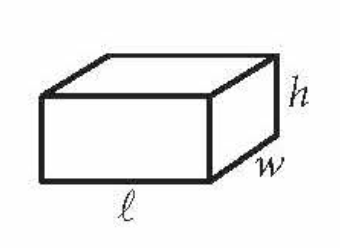
Volume of a Rectangular Prism

lwh

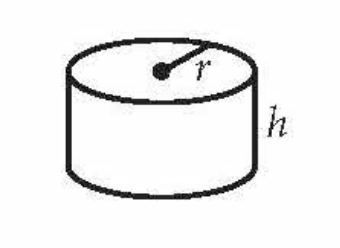
Volume of a Cylinder

πr²h

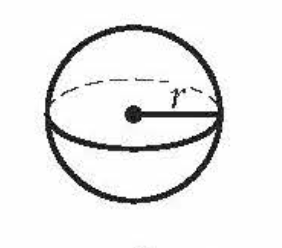
Volume of a Sphere

(4/3)πr³

Volume of a Cone

(1/3)πr²h

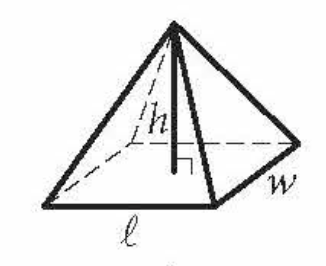
Volume of a Pyramid

(1/3)lwh

The number of degrees of arc in a circle

360.

The number of radians of arc in a circle

2π

The sum of the measures in degrees of the angles of a triangle

180

Kite

two disjoint pairs of consecutive congruent sides

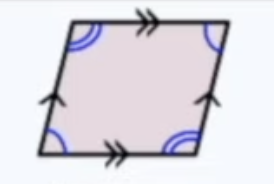
Parallelogram

two pairs of parallel sides

- opposite angles are congruent

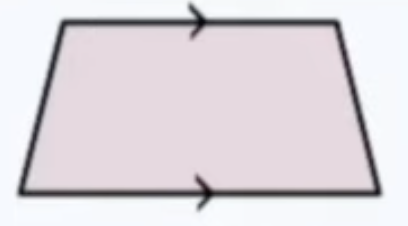
Trapezoid

only one pair of parallel sides

Rectangle

four right angles

Square

four congruent sides and four right angles

Right Triangle

one right angle

Isosceles Triangle

at least two congruent sides

- opposite angles of the congruent sides are congruent

Equilateral Triangle

three congruent sides

- all three angles are congruent (and = 60 degrees)

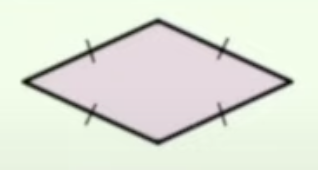
Rhombus

four congruent sides

- opposite angles are congruent

Volume of Prisms

(area of the base)(height)

Surface Area of Prism

area of every single face

- (perimeter of base)h + 2(area of base)

- or calculate area of each face and add

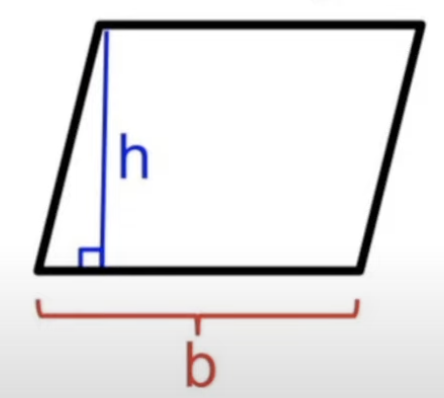
Area of Parallelogram

b(h)

- or, can break up into two triangles and a rectangle, solve that way

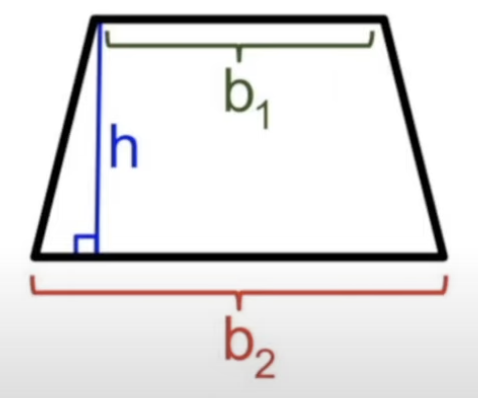
Area of Trapezoid

[(b₁+b₂)/2](height)

- or, can break up into two triangles and a rectangle, solve that way

What does it mean if two shapes are congruent?

They are identical

- same side lengths

- same angle measures

What does it mean if two shapes are similar?

They are proportionate (same shape, but one is bigger or smaller)

- sides are proportionate

- angles are congruent

Conditions sufficient to prove that triangles are congruent

SSS - all sides are congruent

SAS - two sides congruent, angle nestled in between those two sides congruent

ASA - two angles congruent, side nestled in between those angles congruent

AAS - two angles and side congruent (congruent side is opposite the same angle in both triangles)

HL - both right triangles, hypotenuse and leg line up

Conditions sufficient to prove that triangles are similar

AA - two angles are congruent

SAS - two angles are congruent, sides on the outside are proportionate

SSS - all three sides have same proportion

Sum of the Interior Angles of Polygons

(n-2)180

n = number of sides

Sum of the measures of angles in a quadrilateral

360

Sum of the exterior angles of a Polygon

always 360

Degrees to Radians Conversion

180/π

Complementary Angles

x + y = 90

two angles add up to 90 degrees

Supplementary Angles

w + z = 180

two angles add up to 180 degrees

Two Lines are Parallel, Transversal (line drawn through them)

Certain angle relationships emerge

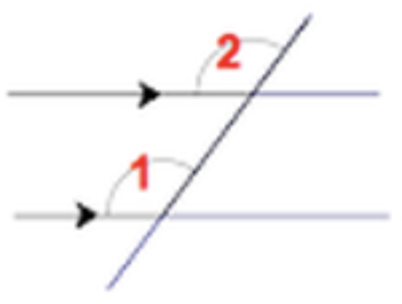
Corresponding Angles (congruent)

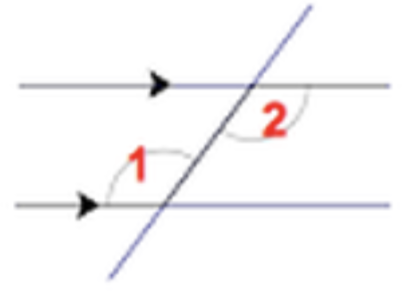
Alternate Interior Angles (congruent)

Alternate Exterior Angles (congruent)

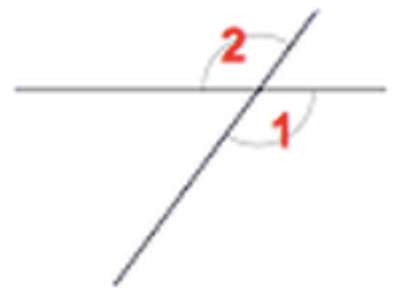
Vertical Angles (congruent)

Consecutive Interior Angles

- add to 180

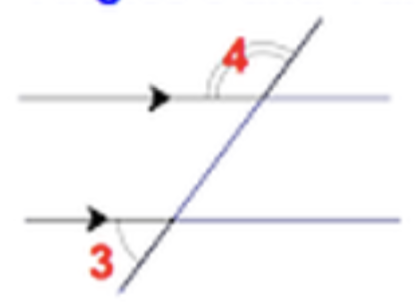
Consecutive Exterior Angles

- add to 180

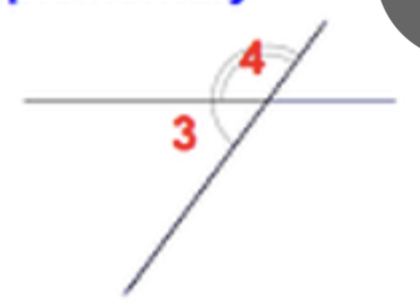
Linear Pair

- add to 180

Sine of an angle

Opposite/Hypotenuse

- never greater than 1 or less than -1

Cosine of an angle

Adjacent/Hypotenuse

- never greater than 1 or less than -1

Tangent of an angle

Opposite/Adjacent

sin(x)=

cos(90-x)

cosine of the complement

Quadrant 1

0<angle<90

0<angle<(π/2)

- everything is positive

Quadrant 2

90<angle<180

(π/2)<angle<(π)

- only sine is positive

Quadrant 3

180<angle<270

(π)<angle<(3π/2)

- only tangent is positive

Quadrant 4

270<angle<360

(3π/2)<angle<(2π)

- only cosine is positive

Unit Circle (Q1)

sin(angle) = y

cos(angle)= x

tan(angle) = y/x

30 degrees, (π/6) - (√3/2 , 1/2)

45 degrees, (π/4) - (√2/2, √2/2)

60 degrees, (π/3)- (1/2, √3/2)

Arc Length

(n/360)(2πr)

or (radius)(central angle in radians)

Area of a Sector

(n/360)(πr²)

or (1/2)(angle in radians)r²

Arc Measure

can be in degrees or radians

equivalent to central angle

double the inscribed angle (or arc length is half of inscribed angle)

Circle Equation

(x-h)² + (y-k)²= r²

(h,k) = center

r = radius

Completing the Square

c=(b/2)²

Equations with one solution

simplify to x=a

Equations with no solutions

a=b

Equations with infinitely many solutions

x=x

slope

(y₂-y₁)/(x₂-x₁)

parallel lines have

same slope

perpendicular lines have

opposite reciprocal slopes

Equations with DIFFERENT slopes (m-values)

the system has one solution

Equations with SAME slope (m-value) but DIFFERENT y-intercepts (b-value)

the system has no solutions

Equations with same slope and y-intercept (m and b values)

the system has infinitely many solutions

More than c, greater than c, OR higher than c

>c

Less than c OR lower than c

<c

greater than or equal to c OR at least c

- no less than c

≥c

less than or equal to c OR at most c

- no more than c

≤c

least, lowest, or minimum value

the lowest value that satisfies the inequality

greatest, highest, or maximum value

the largest value that satisfies the inequality

a possible value

any value that satisfies the inequality

distance=

(rate)(time)

percent

parts per hundred

p%={p}/{100}

what means

x

is means

=

of means

multiplied by

percent means

divided by 100

the sum of all parts of a whole is

100%

Percent Change

(final - initial/initial)x 100

Compounding Annually - Formula

exponential growth

A=P(1±r)^t

Compounding Non-Annually - Formula

exponential growth

A=P(1±r/n)^nt

Simple Interest

A=Prt

Distance Formula

√(x₂-x₁)²+(y₂-y₁)²

Midpoint Formula

((x₁+x₂)/2),((y₁+y₂)/2)

Vertex of a Parabola (in standard form)

-b/2a

Students Selected at Random

Subjects Randomly Assigned to Treatments

• results can be generalized to the entire population
• conclusions about cause and effect can appropriately be drawn

Students Selected at Random

Subjects not Randomly Assigned to Treatments

• results can be generalized to the entire population
• conclusions about cause and effect should not be drawn

Students Not Selected at Random

Subjects Randomly Assigned to Treatments

• results cannot be generalized to entire population
• conclusions about cause and effect can appropriately be drawn

Students Not Selected at Random

Subjects Not Randomly Assigned to Treatments

• results cannot be generalized to the entire population
• conclusions about cause and effect should not be drawn

Percentage Increase

new/original = ( 100 + % ) / 100

shortcut: find x% of the value and add it to x

1.(percent as a decimal)x or x((percent as decimal) + 1)

Percentage Decrease

new/original = ( 100 - % ) / 100

shortcut: x((percent as decimal) - 1)

Proportionality in Circle

arc length/circumference = central angle/360 degrees = area of a sector/area of a circle

Complementary Property of Trig Ratios

sin(x)=cos(90-x)

cos(x)=sin(90-x)