Instructions for Side by Side Printing
- Print the notecards
- Fold each page in half along the solid vertical line
- Cut out the notecards by cutting along each horizontal dotted line
- Optional: Glue, tape or staple the ends of each notecard together
DSAT MATH
front 1 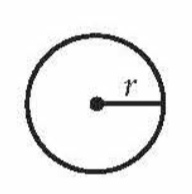 Area of a Circle | back 1 πr2 |
front 2  Circumference of a Circle | back 2 2πr |
front 3 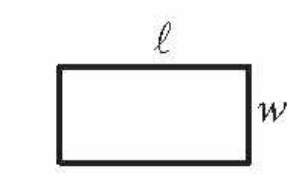 Area of a Rectangle | back 3 lw |
front 4 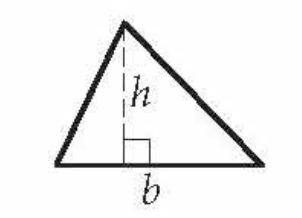 Area of a Triangle | back 4 (1/2)bh |
front 5 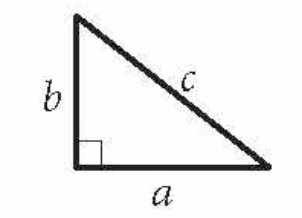 Pythagorean Theorem | back 5 c2=a2+b2 |
front 6 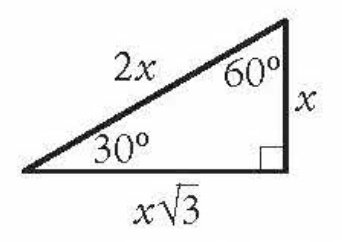 Special Right Triangle | back 6 Across from 30 - x Across from 60 - x√3 Across from 90 - 2x |
front 7 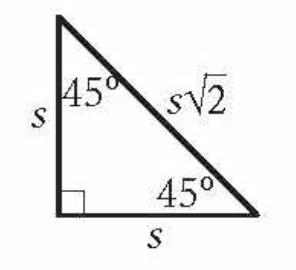 Special Right Triangle | back 7 Across from 45 - s Across from 90 - s√2 |
front 8 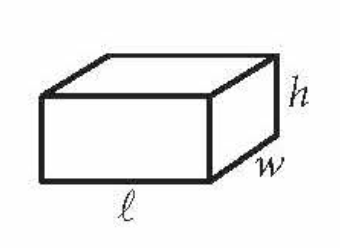 Volume of a Rectangular Prism | back 8 lwh |
front 9 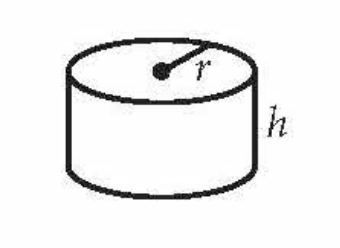 Volume of a Cylinder | back 9 πr2h |
front 10 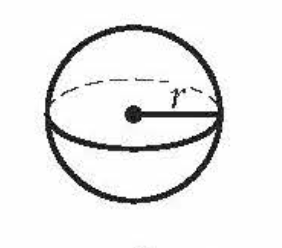 Volume of a Sphere | back 10 (4/3)πr3 |
front 11  Volume of a Cone | back 11 (1/3)πr2h |
front 12 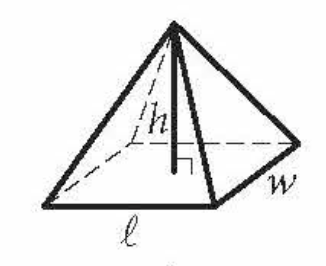 Volume of a Pyramid | back 12 (1/3)lwh |
front 13 The number of degrees of arc in a circle | back 13 360. |
front 14 The number of radians of arc in a circle | back 14 2π |
front 15 The sum of the measures in degrees of the angles of a triangle | back 15 180 |
front 16  Kite | back 16 two disjoint pairs of consecutive congruent sides |
front 17 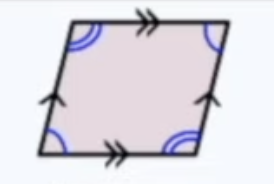 Parallelogram | back 17 two pairs of parallel sides - opposite angles are congruent |
front 18 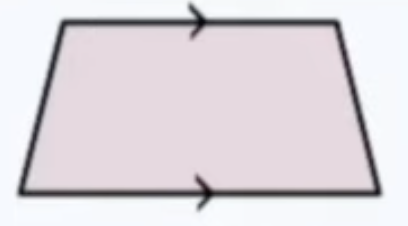 Trapezoid | back 18 only one pair of parallel sides |
front 19  Rectangle | back 19 four right angles |
front 20  Square | back 20 four congruent sides and four right angles |
front 21  Right Triangle | back 21 one right angle |
front 22  Isosceles Triangle | back 22 at least two congruent sides - opposite angles of the congruent sides are congruent |
front 23  Equilateral Triangle | back 23 three congruent sides - all three angles are congruent (and = 60 degrees) |
front 24 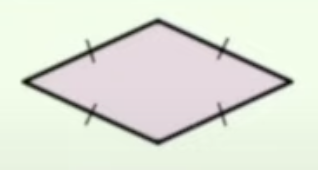 Rhombus | back 24 four congruent sides - opposite angles are congruent |
front 25 Volume of Prisms | back 25 (area of the base)(height) |
front 26 Surface Area of Prism | back 26 area of every single face - (perimeter of base)h + 2(area of base) - or calculate area of each face and add |
front 27 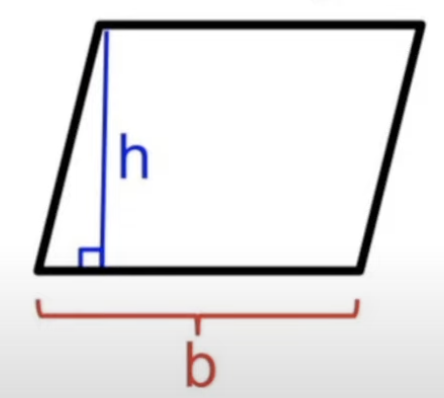 Area of Parallelogram | back 27 b(h) - or, can break up into two triangles and a rectangle, solve that way |
front 28 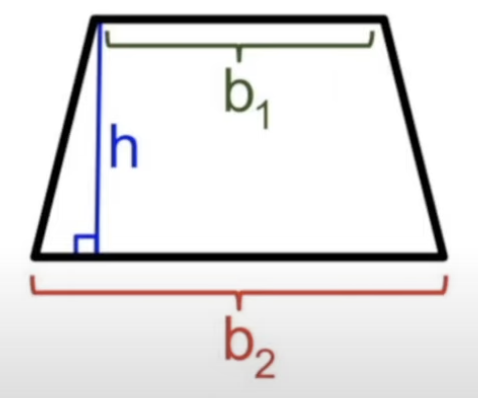 Area of Trapezoid | back 28 [(b1+b2)/2](height) - or, can break up into two triangles and a rectangle, solve that way |
front 29 What does it mean if two shapes are congruent? | back 29 They are identical - same side lengths - same angle measures |
front 30 What does it mean if two shapes are similar? | back 30 They are proportionate (same shape, but one is bigger or smaller) - sides are proportionate - angles are congruent |
front 31 Conditions sufficient to prove that triangles are congruent | back 31 SSS - all sides are congruent SAS - two sides congruent, angle nestled in between those two sides congruent ASA - two angles congruent, side nestled in between those angles congruent AAS - two angles and side congruent (congruent side is opposite the same angle in both triangles) HL - both right triangles, hypotenuse and leg line up |
front 32 Conditions sufficient to prove that triangles are similar | back 32 AA - two angles are congruent SAS - two angles are congruent, sides on the outside are proportionate SSS - all three sides have same proportion |
front 33 Sum of the Interior Angles of Polygons | back 33 (n-2)180 n = number of sides |
front 34 Sum of the measures of angles in a quadrilateral | back 34 360 |
front 35 Sum of the exterior angles of a Polygon | back 35 always 360 |
front 36 Degrees to Radians Conversion | back 36 180/π |
front 37 Complementary Angles | back 37 x + y = 90 two angles add up to 90 degrees |
front 38 Supplementary Angles | back 38 w + z = 180 two angles add up to 180 degrees |
front 39 Two Lines are Parallel, Transversal (line drawn through them) | back 39 Certain angle relationships emerge |
front 40 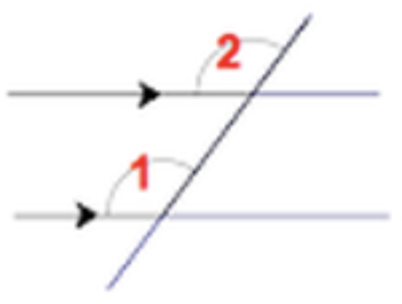 | back 40 Corresponding Angles (congruent) |
front 41 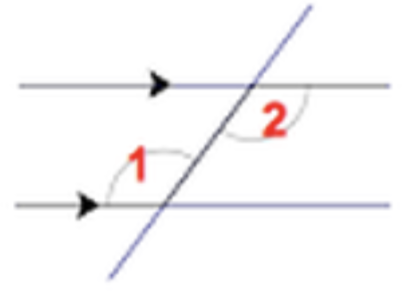 | back 41 Alternate Interior Angles (congruent) |
front 42  | back 42 Alternate Exterior Angles (congruent) |
front 43 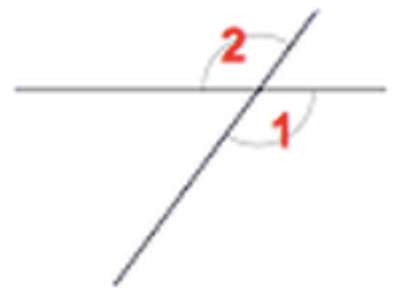 | back 43 Vertical Angles (congruent) |
front 44  | back 44 Consecutive Interior Angles - add to 180 |
front 45 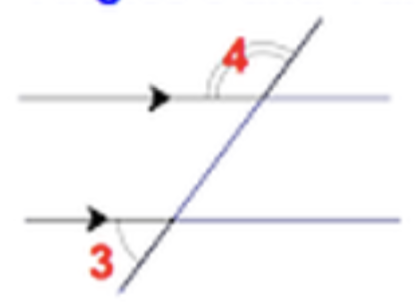 | back 45 Consecutive Exterior Angles - add to 180 |
front 46 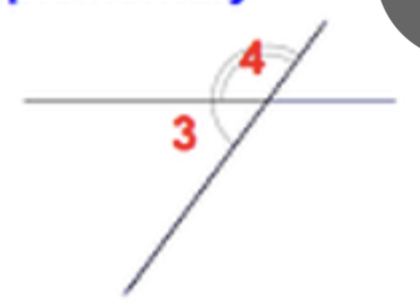 | back 46 Linear Pair - add to 180 |
front 47 Sine of an angle | back 47 Opposite/Hypotenuse - never greater than 1 or less than -1 |
front 48 Cosine of an angle | back 48 Adjacent/Hypotenuse - never greater than 1 or less than -1 |
front 49 Tangent of an angle | back 49 Opposite/Adjacent |
front 50 sin(x)= | back 50 cos(90-x) cosine of the complement |
front 51 Quadrant 1 | back 51 0<angle<90 0<angle<(π/2) - everything is positive |
front 52 Quadrant 2 | back 52 90<angle<180 (π/2)<angle<(π) - only sine is positive |
front 53 Quadrant 3 | back 53 180<angle<270 (π)<angle<(3π/2) - only tangent is positive |
front 54 Quadrant 4 | back 54 270<angle<360 (3π/2)<angle<(2π) - only cosine is positive |
front 55 Unit Circle (Q1) sin(angle) = y cos(angle)= x tan(angle) = y/x | back 55 30 degrees, (π/6) - (√3/2 , 1/2) 45 degrees, (π/4) - (√2/2, √2/2) 60 degrees, (π/3)- (1/2, √3/2) |
front 56 Arc Length | back 56 (n/360)(2πr) or (radius)(central angle in radians) |
front 57 Area of a Sector | back 57 (n/360)(πr2) or (1/2)(angle in radians)r2 |
front 58 Arc Measure | back 58 can be in degrees or radians equivalent to central angle double the inscribed angle (or arc length is half of inscribed angle) |
front 59 Circle Equation | back 59 (x-h)2 + (y-k)2= r2 (h,k) = center r = radius |
front 60 Completing the Square | back 60 c=(b/2)2 |
front 61 Equations with one solution | back 61 simplify to x=a |
front 62 Equations with no solutions | back 62 a=b |
front 63 Equations with infinitely many solutions | back 63 x=x |
front 64 slope | back 64 (y2-y1)/(x2-x1) |
front 65 parallel lines have | back 65 same slope |
front 66 perpendicular lines have | back 66 opposite reciprocal slopes |
front 67 Equations with DIFFERENT slopes (m-values) | back 67 the system has one solution |
front 68 Equations with SAME slope (m-value) but DIFFERENT y-intercepts (b-value) | back 68 the system has no solutions |
front 69 Equations with same slope and y-intercept (m and b values) | back 69 the system has infinitely many solutions |
front 70 More than c, greater than c, OR higher than c | back 70 >c |
front 71 Less than c OR lower than c | back 71 <c |
front 72 greater than or equal to c OR at least c - no less than c | back 72 ≥c |
front 73 less than or equal to c OR at most c - no more than c | back 73 ≤c |
front 74 least, lowest, or minimum value | back 74 the lowest value that satisfies the inequality |
front 75 greatest, highest, or maximum value | back 75 the largest value that satisfies the inequality |
front 76 a possible value | back 76 any value that satisfies the inequality |
front 77 distance= | back 77 (rate)(time) |
front 78 percent | back 78 parts per hundred p%={p}/{100} |
front 79 what means | back 79 x |
front 80 is means | back 80 = |
front 81 of means | back 81 multiplied by |
front 82 percent means | back 82 divided by 100 |
front 83 the sum of all parts of a whole is | back 83 100% |
front 84 Percent Change | back 84 (final - initial/initial)x 100 |
front 85 Compounding Annually - Formula exponential growth | back 85 A=P(1±r)t |
front 86 Compounding Non-Annually - Formula exponential growth | back 86 A=P(1±r/n)nt |
front 87 Simple Interest | back 87 A=Prt |
front 88 Distance Formula | back 88 √(x2-x1)2+(y2-y1)2 |
front 89 Midpoint Formula | back 89 ((x1+x2)/2),((y1+y2)/2) |
front 90 Vertex of a Parabola (in standard form) | back 90 -b/2a |
front 91 Students Selected at Random Subjects Randomly Assigned to Treatments | back 91
|
front 92 Students Selected at Random Subjects not Randomly Assigned to Treatments | back 92
|
front 93 Students Not Selected at Random Subjects Randomly Assigned to Treatments | back 93
|
front 94 Students Not Selected at Random Subjects Not Randomly Assigned to Treatments | back 94
|
front 95 Percentage Increase | back 95 new/original = ( 100 + % ) / 100 shortcut: find x% of the value and add it to x 1.(percent as a decimal)x or x((percent as decimal) + 1) |
front 96 Percentage Decrease | back 96 new/original = ( 100 - % ) / 100 shortcut: x((percent as decimal) - 1) |
front 97 Proportionality in Circle | back 97 arc length/circumference = central angle/360 degrees = area of a sector/area of a circle |
front 98 Complementary Property of Trig Ratios | back 98 sin(x)=cos(90-x) cos(x)=sin(90-x) |