Correlation coefficients (p) range from …

-1 to +1

Correlation coefficient (p) of -1 implies...

perfectly negative correlation

Correlation coefficient (p) of +1 implies...

perfectly positive correlation

Correlation coefficient (p) of 0 implies...

variables are not related

Why is the T-bill return independent of the economy? Do T-bills promise a completely risk-free return?

• T-bills will return the promised return (nominal) regardless of the economy.
• No, T-bills do not provide a risk-free return, as they are still exposed to inflation. Although, very little unexpected inflation is likely to occur over such a short period of time.
• T-bills are also risky in terms of reinvestment rate risk.
• T-bills are risk-free in the default and liquidity sense of the word.

Describe the correlations of these two graphs

Left graph - perfectly positively correlated returns (p = +1)

Right graph - perfectly negatively correlated returns (p = -1)

What effect does adding stocks have on:

1. Standard deviation (σ)
2. Expected return of portfolio
3. Diversification benefits

1. σ_p decreases as stocks added, because they wod not be perfectly correlated with the existing portfolio.
2. Expected return of the portfolio would remain relatively constant.
3. Eventually the diversification benefits of adding more stocks dissipates (after about 40 stocks), and for large stock portfolios, σ_p tends to converge to ~20%.

After about ________stocks, the diversification benefits of adding more stocks dissipates

40

1. What are some examples of company-specific risk?
2. What are some other names for company specific risk?

1. Natural disasters, accidents, strikes, lawsuits, death of CEO
2. Diversifiable, Idiosyncratic, Un-Systematic

1. What are some examples of market risk?
2. What are some other names for market risk?

1. Inflation, recession, war, yield inversion etc.
2. Non-Diversifiable, Systematic

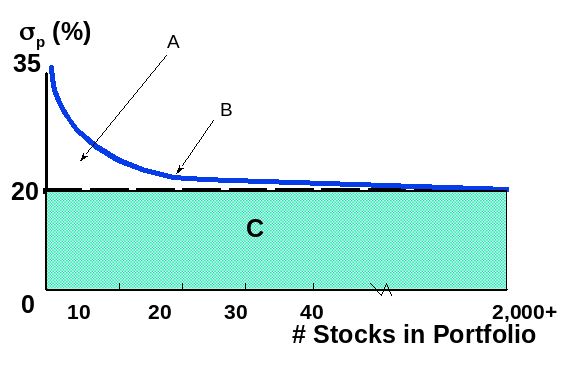Label the following graph

1. Company-specific risk
2. Total risk, σ_p
3. Market risk

1. __________ risk – portion of a security’s stand-alone risk that cannot be eliminated through diversification. Measured by beta.
2. __________ risk – portion of a security’s stand-alone risk that can be eliminated through proper diversification.

1. Market risk
2. Firm-specific

If an investor chooses to hold a one-stock portfolio (exposed to more risk than a diversified investor), would the investor be compensated for the risk they bear?

• No!
• Stand-alone risk is not important to a well-diversified investor – because it vaporizes
• Rational, risk-averse investors are concerned with σp, which is based upon market risk.
• There can be only one price (the market return) for a given security.
• No compensation should be earned for holding unnecessary, diversifiable risk.

Do most stocks have positive, negative or zero betas?

Positive

Market beta is 1 by definition

1. If beta is ____, the security is just as risky as the average stock.
2. If beta is _____, the security is riskier than average.
3. If beta is _____, the security is less risky than average.
4. Most stocks have betas in the range of ______.

(all the answers are numbers)

1. = 1.0
2. >1.0
3. <1.0
4. 0.5 to 1.5

For a beta of +2, if …

1. Market goes up 1%, stock expected to _________.
2. Market goes down 1%, stock __________.
3. What does this mean in terms of risk?

1. go up 2%
2. goes down 2%
3. stock is twice as risky as the market

Which of the following statements are correct?

1. diversifiable risk can be eliminated by proper diversification
2. market risk cannot be eliminated by proper diversification
3. the market portfolio has risk
4. all of the above are correct

D - Diversifiable risk can be eliminated by proper diversification, while market risk cannot be eliminated by proper diversification.

1. Incorrect choice. This is true, but it is also true that market risk cannot be eliminated by proper diversification.
2. Incorrect choice. This is true, but it is also true that diversifiable risk can be eliminated by proper diversification.
3. Incorrect choice. This is true . The market portfolio has no diversifiable risk, but still has risk that cannot be eliminated through diversification (market risk).

Which of the following statements best describes what would be expected to happen as you randomly add stocks to your portfolio?

1. Adding more stocks to your portfolio reduces the portfolio’s company-specific risk.
2. Adding more stocks to your portfolio reduces the beta of your portfolio.
3. Adding more stocks to your portfolio increases the portfolio’s expected return.

A - If stock returns are not perfectly correlated, adding more stocks to your portfolio should reduce the portfolio’s company specific risk.

1. Correct
2. Incorrect choice. Market risk (which is measured by beta) can go up, down, or remain unchanged as new stocks are added.
3. Incorrect choice. Expected return can go up, down, or remain unchanged as new stocks are added.

___________ is a measure of market risk which is the extent to which the returns on a stock move with the market.

1. Beta
2. Standard deviation
3. Coefficient of variation
4. Expected return

A - Correct. Beta is a measure of market risk which is the extent to which the returns on a stock move with the market.

What is the proxy for the risk-free rate?

U.S. Treasury Bills

What is the proxy for the return on the market?

Typically use the S&P500 Index

What is the typical range for the market risk premium?

4-8% per year

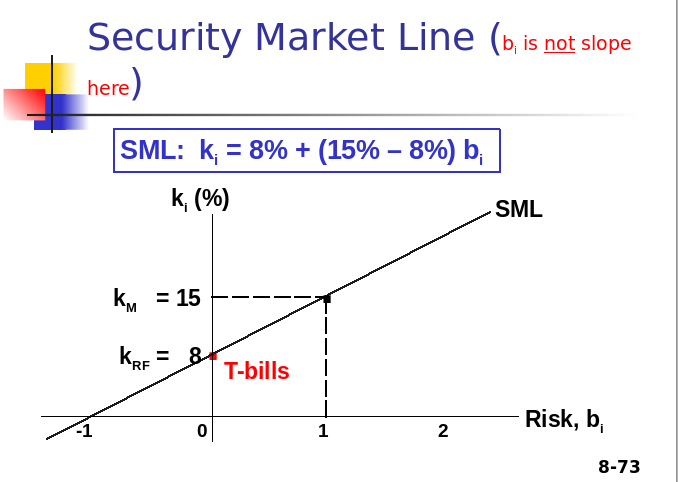What is the slope of this line, and what does it represent?

7%

Risk premium

What happens to prices if investors raise inflation expectations by 3%?

Reqd return on all risky assets increases by 3%, Prices drop

If Expected Return increases ->Current Price drops
If Realized Return increases -> Final Price rises

What happens to price if investors’ risk aversion increased, causing the market risk premium to increase by 3% (rise/run=3/1)?

Prices of high Beta stocks drop more

k_m rises from 15 to 18%, so k_i for b=.5 rises by 1.5%, and for b=2 rises by 6%, delta Rf =0

Changes in SML impact riskier stocks more.

1. True
2. False

A

Does a higher required return mean that the actual return you get will be higher?

No, may lose all of your money on a stock, because Realized Return does not equal Expected Return

A high beta port will generate high returns only if _______ is high.

Rm

Investors’ required returns are based on future risk, but betas are calculated with historical data. Will a company’s beta be the same this year and next year?

• No – Non-Stationarity Problem, but drift is small
• Assumes markets are efficient
• There have been studies that both support and dispute the CAPM
• Still used in practice [provides a conceptual framework useful for linking risk and return in financial decisions]
• Use for understanding current portfolio risk rather than forecasting portfolio performance

The CAPM says that the relevant risk of an individual asset is its:

1. stand-alone risk.
2. expected return
3. realized return
4. portfolio or market risk

D - The CAPM say that the relevant risk of an individual asset is its contribution to the risk of a well-diversified portfolio (its portfolio or market risk). How the addition of a stock to the portfolio alters its Beta. The rest is diversified away.

Which of the following statements is correct?

1. It is possible to have a situation in which the market risk of a single stock is less than the market risk of a portfolio of stocks.
2. The market risk premium will increase if, on average, market participants become more risk averse.
3. If you selected a group of stocks whose returns are perfectly positively correlated, then you could end up with a portfolio for which none of the unsystematic risk is diversified away.
4. All of the statements above are correct.

D

Stock A has a beta of 1.0 and Stock B has a beta of 0.8. Which of the following statements must be true about these securities? (Assume the market is in equilibrium.)

1. When held in isolation, Stock A has greater risk than Stock B.
2. Stock B would be a more desirable addition to a portfolio than Stock A.
3. Stock A would be a more desirable addition to a portfolio than Stock B.
4. The expected return on Stock A will be greater than that on Stock B.
5. The expected return on Stock B will be greater than that on Stock A.

D - In equilibrium, Stock A will have a higher expected return to compensate for the additional market risk.

1. Incorrect choice. Beta measures only market risk. In isolation, stand-alone risk measures could show either stock to be more risky since diversifiable risk is included.
2. Incorrect choice. Stock B adds less market risk to the portfolio, but that does not mean that it is more desirable since investors would be compensated for the additional market risk of Stock A.
3. Incorrect choice. Stock A adds more market risk to the portfolio, but that does not mean that it is less desirable since investors would be compensated for the additional market risk.
4. Correct
5. Incorrect choice. In equilibrium, Stock A will have a higher expected return to compensate for the additional market risk.

Is it possible to construct a portfolio of real-world stocks that has a required return equal to the risk-free rate? Explain.

Yes, if the portfolio’s beta is equal to zero. In practice, however, it may be impossible to find individual stocks that have a nonpositive beta. In this case it would also be impossible to have a stock portfolio with a zero beta. Even if such a portfolio could be constructed, investors would probably be better off just purchasing Treasury bills, or other zero beta investments.

Stock A has an expected return of 7%, a standard deviation of expected returns of 35%, a correlation coefficient with the market of −0 3, and a beta coefficient of −0 5. Stock B has an expected return of 12%, a standard deviation of returns of 10%, a 0 7 correlation with the market, and a beta coefficient of 1 0. Which security is riskier? Why?

Security A is less risky if held in a diversified portfolio because of its negative correlation with other stocks. In a single-asset portfolio, Security A would be more risky because σ_A > σ _B and CV_A > CV_B.

A stock had a 12% return last year, a year when the overall stock market declined. Does this mean that the stock has a negative beta and thus very little risk if held in a portfolio? Explain.

No. For a stock to have a negative beta, its returns would have to logically be expected to go up in the future when other stocks’ returns were falling. Just because in one year the stock’s return increases when the market declined doesn’t mean the stock has a negative beta. A stock in a given year may move counter to the overall market, even though the stock’s beta is positive.

If a company's beta were to double, would its required return also double?

According to the Security Market Line (SML) equation, an increase in beta will increase a company’s expected return by an amount equal to the market risk premium times the change in beta. For example, assume that the risk-free rate is 6%, and the market risk premium is 5%. If the company’s beta doubles from 0.8 to 1.6 its expected return increases from 10% to 14%. Therefore, in general, a company’s expected return will not double when its beta doubles.

Given the following information, determine the beta coefficient for Stock J that is consistent with equilibrium: r_J = 12.5%, r_RF = 4.5%, r_M = 10.5%.

In equilibrium:

r_J = r_J = 12.5%.

r_J = r_RF + (r_M – r_RF)b

12.5% = 4.5% + (10.5% – 4.5%)b

b = 1.33

Stock R has a beta of 1.5, Stock S has a beta of 0.75, the required return on an average stock is 13%, and the risk-free rate of return is 7%. By how much does the required return on the riskier stock exceed the required return on the less risky stock?

We know that b_R = 1.50, b_S = 0.75, r_M = 13%, r_RF = 7%.

r_i = r_RF + (r_M – r_RF)b_i = 7% + (13% – 7%)b_i.

r_R = 7% + 6%(1.50) = 16.0%

r_S = 7% + 6%(0.75) = 11.5

16.0% - 11.5% = 4.5%

Bradford Manufacturing Company has a beta of 1.45, while Farley Industries has a beta of 0.85. The required return on an index fund that holds the entire stock market is 12.0%. The risk-free rate of interest is 5%. By how much does Bradford’s required return exceed Farley’s required return?

An index fund will have a beta of 1.0. If r_M is 12.0% (given in the problem) and the risk-free rate is 5%, you can calculate the market risk premium (RP_M) calculated as r_M – r_RF as follows:

r = r_RF + (RP_M)b

12.0% = 5% + (RP_M)1.0

7.0% = RP_M

Required Return = R_RF + (R_PM ) x beta
Return for Bradford = 5% + (7%) x 1.45 = 15.15%
Required return for Farley = 5% + (7%) X 0.85 = 10.95%
15.15% - 10.95% = 4.2%
Bradford's required return exceeds Farley's by 4.2%

Calculate the required rate of return for Manning Enterprises, assuming that investors expect a 3.5% rate of inflation in the future. The real risk-free rate is 2.5% and the market risk premium is 6.5%. Manning has a beta of 1.7, and its realized rate of return has averaged 13.5% over the past 5 years.

r_RF = r* + IP = 2.5% + 3.5% = 6%.

r_s = 6% + (6.5%)1.7 = 17.05%.

Suppose r_RF=9%, r_M=14%, and b_i=1.3.

What is r_i, the required rate of return on Stock i ?

r_i = r_RF + (r_M – r_RF)b_i = 9% + (14% – 9%)1.3 = 15.5%.

Suppose r_RF=9%, r_M=14%, and b_i=1.3.

Now suppose that r_RF (1) increases to 10% or (2) decreases to 8%. The slope of the SML remains constant. How would this affect r_M and r_i ?

1. r_RF increases to 10%:

r_M increases by 1 percentage point, from 14% to 15%.

r_i = r_RF + (r_M – r_RF)b_i = 10% + (15% – 10%)1.3 = 16.5%.

2. r_RF decreases to 8%:

r_M decreases by 1%, from 14% to 13%.

r_i = r_RF + (r_M – r_RF)b_i = 8% + (13% – 8%)1.3 = 14.5%.

Suppose r_RF=9%, r_M=14%, and b_i=1.3.

Now assume that r_RF remains at 9% but r_M (1) increases to 16% or (2) falls to 13%. The slope of the SML does not remain constant. How would these changes affect r_i ?

1. r_M increases to 16%:

r_i = r_RF + (r_M – r_RF)b_i = 9% + (16% – 9%)1.3 = 18.1%.

2. r_M decreases to 13%:

r_i = r_RF + (r_M – r_RF)b_i = 9% + (13% – 9%)1.3 = 14.2%.

Consider the following information for three stocks, Stocks X, Y, and Z. The returns on the three stocks are positively correlated, but they are not perfectly correlated. (That is, each of the correlation coefficients is between 0 and 1.). Fund P has half of its funds invested in Stock X and half invested in Stock Y. Fund Q has one-third of its funds invested in each of the three stocks. The risk-free rate is 5.5%, and the market is in equilibrium. (That is, required returns equal expected returns.) What is the market risk premium ( r M - r RF )?

Using Stock X (or any stock):

9% = r_RF + (r_M – r_RF)b_X

9% = 5.5% + (r_M – r_RF)0.8

(r_M – r_RF) = 4.375%.

Stock X has a 10% expected return, a beta coefficient of 0.9, and a 35% standard deviation of expected returns. Stock Y has a 12.5% expected return, a beta coefficient of 1.2, and a 25% standard deviation. The risk-free rate is 6%, and the market risk premium is 5%. Calculate each stock's coefficient of variation.

r_x = 10%; b_X = 0.9; σ_X = 35%.

r_y = 12.5%; b_Y = 1.2; σ_Y = 25%.

r_RF = 6%; RP_M = 5%.

CV_X = 35%/10% = 3.5. CV_Y = 25%/12.5% = 2.0.

Stock X has a 10% expected return, a beta coefficient of 0.9, and a 35% standard deviation of expected returns. Stock Y has a 12.5% expected return, a beta coefficient of 1.2, and a 25% standard deviation. The risk-free rate is 6%, and the market risk premium is 5%. Which stock is riskier for a diversified investor?

For diversified investors the relevant risk is measured by beta. Therefore, the stock with the higher beta is more risky. Stock Y has the higher beta so it is more risky than Stock X.

Stock X has a 10% expected return, a beta coefficient of 0.9, and a 35% standard deviation of expected returns. Stock Y has a 12.5% expected return, a beta coefficient of 1.2, and a 25% standard deviation. The risk-free rate is 6%, and the market risk premium is 5%. Calculate each stock's required rate of return. On the basis of the two stock's expected and required returns, which stock would be more attractive to a diversified investor?

r_X = 6% + 5%(0.9)

= 10.5%.

r_Y = 6% + 5%(1.2)

= 12%.

Stock Y would be most attractive to a diversified investor since its expected return of 12.5% is greater than its required return of 12%.

Stock X has a 10% expected return, a beta coefficient of 0.9, and a 35% standard deviation of expected returns. Stock Y has a 12.5% expected return, a beta coefficient of 1.2, and a 25% standard deviation. The risk-free rate is 6%, and the market risk premium is 5%. Calculate the required return of a portfolio that has$7,500 invested in Stock X and $2,500 invested in Stock Y?

b_p = ($7,500/$10,000)0.9 + ($2,500/$10,000)1.2

= 0.6750 + 0.30

= 0.9750.

r_p = 6% + 5%(0.975)

= 10.875%.

Stock X has a 10% expected return, a beta coefficient of 0.9, and a 35% standard deviation of expected returns. Stock Y has a 12.5% expected return, a beta coefficient of 1.2, and a 25% standard deviation. The risk-free rate is 6%, and the market risk premium is 5%. If the market risk premium increased to 6 percent, which of the two stocks would have the larger increase in its requiredreturn?

If RP_M increases from 5% to 6%, the stock with the highest beta will have the largest increase in its required return. Therefore, Stock Y will have the greatest increase.

Check:

r_X = 6% + 6%(0.9)

= 11.4%. Increase 10.5% to 11.4%.

r_Y = 6% + 6%(1.2)

= 13.2%. Increase 12% to 13.2%.

The values of outstanding bonds change whenever the going rate of interest changes. In general, short-term interest rates are more volatile than long-term interest rates. Therefore, short-term bond prices are more sensitive to interest rate changes than are long-term bond prices. Is that statement true or false? Explain. (Hint: Make up a "reasonable" example based on a 1-year and a 20-year bond to help answer the question.)

False. Short-term bond prices are less sensitive than long-term bond prices to interest rate changes because funds invested in short-term bonds can be reinvested at the new interest rate sooner than funds tied up in long-term bonds.

For example, consider two bonds, both with a 10% annual coupon and a $1,000 par value. The only difference between them is their maturity. One bond is a 1-year bond, while the other is a 20-year bond. Consider the values of each at 5%, 10%, 15%, and 20% interest rates.

1-year 20-year

5% $1,047.62 $1,623.11

10% 1,000.00 1,000.00

15% 956.52 687.03

20% 916.67 513.04

As you can see, the price of the 20-year bond is much more volatile than the price of the 1-year bond.

If interest rates rise after a bond issue, what will happen to the bond's price and YTM? Does the time to maturity affect the extent to which interest rate changes affect the bond's price? (Again, an example might help you answer this question.)

The price of the bond will fall and its YTM will rise if interest rates rise. If the bond still has a long term to maturity, its YTM will reflect long-term rates. Of course, the bond’s price will be less affected by a change in interest rates if it has been outstanding a long time and matures shortly. While this is true, it should be noted that the YTM will increase only for buyers who purchase the bond after the change in interest rates and not for buyers who purchased previous to the change. If the bond is purchased and held to maturity, the bondholder’s YTM will not change, regardless of what happens to interest rates. For example, consider two bonds with an 8% annual coupon and a $1,000 par value. One bond has a 5-year maturity, while the other has a 20-year maturity. If interest rates rise to 15% immediately after issue the value of the 5-year bond would be $765.35, while the value of the 20-year bond would be $561.85.

Assume that you have a short investment horizon (less than 1 year). You are considering two investments: a 1-year Treasury security and a 20-year Treasury security. Which of the two investments would you view as being riskier? Explain.

As an investor with a short investment horizon, I would view the 20-year Treasury security as being more risky than the 1-year Treasury security. If I bought the 20-year security, I would bear a considerable amount of interest rate risk. Since my investment horizon is only one year, I would have to sell the 20-year security one year from now, and the price I would receive for it would depend on what happened to interest rates during that year. However, if I purchased the 1-year security I would be assured of receiving my principal at the end of that one year, which is the 1-year Treasury’s maturity date.

Will the following increase or decrease a bond's yield to maturity: The bond's price increases.

If a bond’s price increases, its YTM decreases.

Will the following increase or decrease a bond's yield to maturity: The bond is downgraded by the rating agencies.

If a company’s bonds are downgraded by the rating agencies, its YTM increases.

Will the following increase or decrease a bond's yield to maturity: A change in the bankruptcy code makes it more difficult for bondholders to receive payments in the event the firm declares bankruptcy.

If a change in the bankruptcy code made it more difficult for bondholders to receive payments in the event a firm declared bankruptcy, then the bond’s YTM would increase.

Will the following increase or decrease a bond's yield to maturity: The economy seems to be shifting from a boom to a recession. Discuss the effects of the firm's credit strength in your answer.

If the economy entered a recession, then the possibility of a firm defaulting on its bond would increase; consequently, its YTM would increase.

Will the following increase or decrease a bond's yield to maturity: Investors learn that the bonds are subordinated to another debt issue.

If a bond were to become subordinated to another debt issue, then the bond’s YTM would increase.

Callaghan Motors bonds have 10 years remaining to maturity. Interest is paid annually, they have a $1,000 par value, the coupon interest rate is 8%, and the yield to maturity is 9%. What is the bond's current market price?

With your financial calculator, enter the following:

N = 10; I/YR = YTM = 9%; PMT = 0.08 ´ 1,000 = 80; FV = 1000; PV = V_B = ?

PV = $935.82.

A bond has a $1,000 par value , 10 years to maturity, and a 7% annual coupon and sells for $985. What is its yield to maturity?

V_B = $985; M = $1,000; Int = 0.07 ´ $1,000 = $70.

Current yield = Annual interest/Current price of bond

= $70/$985.00

= 7.11%.

A bond has a $1,000 par value , 10 years to maturity, and a 7% annual coupon and sells for $985. Assume that the yield to maturity remains constant for the next 3 years. What will the price be 3 years from today?

For N = 10; PV = -985; PMT = 70; FV = 1000; YTM = ?

Solve for I/YR = YTM = 7.2157% » 7.22%.

Now, N = 7 [7 yrs remaining]; I/YR = 7.2157; PMT = 70; FV = 1000; PV = ?

Solve for V_B = PV = $988.46.

Nungesser Corporation's outstanding bonds have a $1,000 par value, a 9% semiannual coupon, 8 years to maturity, and a 8.5% YTM. What is the bond's price?

The problem asks you to find the price of a bond, given the following facts: N = 2 ´ 8 = 16; I/YR = 8.5/2 = 4.25; PMT = 45; FV = 1000.

With a financial calculator, solve for PV = $1,028.60.

Last year Joan purchased a $1,000 face value corporate bond with an 11% annual coupon rate and a 10-year maturity. At the time of purchase, it had an expected yield to maturity if 9.79%. If Joan sold the bond today for $1,060.90, what rate of return would she have earned for the past year?

First, we must find the price Joan paid for this bond.

N = 10, I/YR = 9.79, PMT = 110, FV = 1000

PV = -$1,075.02. V_B = $1,075.02.

Then to find the one-period return, we must find the sum of the change in price and the coupon received divided by the starting price.

One-period return = (Ending price - Beginning price + Coupon received) / Beginning price

One-period return = ($1,060.49 – $1,075.02 + $110)/$1,075.02

One-period return = 8.88%.

Explain whether the following statement is true or false: $100 a year for 10 years is an annuity; but $100 in Year 1, $200 in Year 2, and $400 in Years 3 through 10 does not constitute an annuity. However, the second series contains an annuity.

True. The second series is an uneven cash flow stream, but it contains an annuity of $400 for 8 years. The series could also be thought of as a $100 annuity for 10 years plus an additional payment of $100 in Year 2, plus additional payments of $300 in Years 3 through 10.

If a firm's earnings per share grew from $1 to $2 over a 10-year period, the total growth would be 100%, but the annual growth rate would be less than 10%. True or false? Explain. (Hint: If you aren't sure, plug in some numbers and check it out.)

True, because of compounding effects—growth on growth. The following example demonstrates the point. The annual growth rate is I in the following equation:

$1(1 + I)¹⁰ = $2.

We can find I in the equation above as follows:

Using a financial calculator input N = 10, PV = -1, PMT = 0, FV = 2, and I/YR = ? Solving for I/YR you obtain 7.18%.

Viewed another way, if earnings had grown at the rate of 10% per year for 10 years, then EPS would have increased from $1.00 to $2.59, found as follows: Using a financial calculator, input N = 10, I/YR = 10, PV = -1, PMT = 0, and FV = ?. Solving for FV you obtain $2.59. This formulation recognizes the “interest on interest” phenomenon.

Would you rather have a savings account that pays 5% interest compounded semiannually or one that pays 5% interest compounded daily? Explain.

For the same stated rate, daily compounding is best. You would earn more “interest on interest.”

If you deposit $10,000 in a bank account that pays 10% interest annually, how much will be in your account after 5 years?

FV₅ = $10,000(1.10)⁵

= $10,000(1.61051) = $16,105.10.

Alternatively, with a financial calculator enter the following: N = 5, I/YR = 10, PV = -10000, and PMT = 0. Solve for FV = $16,105.10.

What is the present value of an investment security that will pay $5,000 in 20 years if securities of equal risk available on the market pay 7% annually?

With a financial calculator enter the following: N = 20, I/YR = 7, PMT = 0, and FV = 5000. Solve for PV = $1,292.10.

Your parents will retire in 18 years. They currently have $250,000, and they think that they will need $1,000,000 at retirement. What interest rate must they earn to reach their goal (assuming they will not save any additional funds)?

With a financial calculator enter the following: N = 18, PV = -250000, PMT = 0, and FV = 1000000. Solve for I/YR = 8.01% ≈ 8%.

If you deposit money today in an account that pays 6.5% annual interest, how long will it take to double your money?

Time to double your money: Rule of 72 (72/6.5=11yrs, 72/11=6.5%)

2 = 1(1.065)ⁿ.

With a financial calculator enter the following: I = 6.5, PV = -1, PMT = 0, and FV = 2. Solve for N = 11.01 ≈ 11 years

You have $42,180.53 in a brokerage account, and you plan to deposit an additional $5,000 at the end of every future year until your account totals $250,000. You expect to earn 12% annually on the account. How many years will it take to reach your future goal?

Using your financial calculator, enter the following data: I/YR = 12; PV = ‑42180.53; PMT = ‑5000; FV = 250000; N = ? Solve for N = 11. It will take 11 years to accumulate $250,000.

What is the future value of a 7%, 5-year ordinary annuity that pays $300 each year? If this were an annuity due, what would its future value be?

With a financial calculator enter the following: N = 5, I/YR = 7, PV = 0, and PMT = 300. Solve for FV = $1,725.22.

With a financial calculator, switch to “BEG” and enter the following: N = 5, I/YR = 7, PV = 0, and PMT = 300. Solve for FV = $1,845.99. Don’t forget to switch back to “END” mode.

What do we call the value of a cash flow today?

Present Value or Principal

Let’s say you have $100 in an account which earns 10 % annually. How much would you have after one year?

Take $100 and multiply by 1.10 = $100 (1.10) = $110

Let’s say you have $100 in an account which earns 10 % annually. How much would you have after two years??

$110 (1.10) = $100 (1.10)(1.10) = $100 (1.10)²

You put $1000 into a retirement account paying 8% annually for 37 years. What do you end up with?

FV37 = 1000(1.08)³⁷ = $17,245.63

You invest $300 in an account paying 11% interest. How much will you have in 6 years?

$561.12

You put $400 into an account that pays 8 % interest compounded annually, quarterly.

1. How much will be in your account in 6 years?
2. What do you get if you compound daily instead?

a. $643.37

b. = $646.40

See Chapter 5, slide 2-16 for explanation

Will the FV of a lump sum be larger or smaller if compounded more often, holding the stated I% constant?

LARGER, as the more frequently compounding occurs, interest is earned on interest more often

What is the future value for $100 @ 10% for 3 years.

1. Compounded annually
2. Compounded semi-annually

1. $133.10
2. $134.01

See Chapter 5, slide 2-17 for explanation

The effective rate (i_eff) will always be ________(lesser/greater) than the nominal rate if the compounding frequency is greater than one time per year

greater

The ______ rate is commonly called the annual percentage rate (or APR)

nominal

The ______ rate is commonly called the annual percentage yield (or APY)

effective annual rate (true rates)

_______ rates - contractual rates of interest charged by a lender or promised by a borrower

nominal rates (APR)

_______ rates - rates of interest actually paid or earned

Effective annual rates (true rates) (APY)

1. k_simple = _______ (APR or APY)
2. EAR (effective annual rate) = _______ (APR or APY)

1. APR
2. APY

What is the EAR for a simple rate of 10%, compounded semi-annually?

10.25%

See chapter 5, slide 2-21 for explanation

What is the effective annual rate of 12%, compounded monthly?

[1+.12/12]^12-1 = EAR = 12.68%

What is the effective annual rate of 12%, compounded daily?

[1+.12/365]^365-1 = EAR = 12.75%

Can the effective rate ever be equal to the nominal rate?

• Yes, but only if annual compounding is used, i.e., if m = 1.
• If m > 1, EFF% will always be greater than the nominal rate.

Suppose you put $100 in your account every year for 3 years, earning 7% interest. How much would you have after the 3 years?

$321.49

3 years $100 ordinary annuity

Suppose you put $100 in your account every year for 3 years, earning 7% interest. How much would you have after the 3 years?

You must calculate each payment separately because they have been in the account for a different number of years.

FV3 = 100(1.07)² + 100(1.07)¹ + 100

FV3 = $321.49

ALSO PV3=$262.43, when FV=0

Chapter 5, slide 2-26

What is the difference between an ordinary annuity and an annuity due?

• Regular Annuity - payment made at the end of each time period
• Annuity Due - payment made at the beginning of each time period

Suppose you need $20,000 in three years to buy your new hybrid car. If you can earn 8% on your money, how much do you need today?

PV = 20,000 / (1.08)3 = $15,876

Chapter 5, slide 2-31

What happens to PV if the interest rate is increased??

It decreases

What happens to PV if the investment term increases??

It decreases

Suppose you want to have enough money in your bank account to withdraw $800 at the end of each year for three years in order to pay tuition. How much money should you have in the account now if you can earn 9% interest??

$2,025.04

Chapter 5, slide 2-34

Suppose you need $15,000 in 20 years to pay for a ski trip. If you can earn 9% on your money, how much do you need today [lump sum]?

$2676.46 today

Chapter 5, slide 2-35

Suppose you need $15,000 in 20 years to pay for a ski trip. If you can earn 9% on your money, how much do you need to deposit annually?

$293.20/yr

Chapter 5, slide 2-35

Suppose you need $15,000 in 20 years to pay for a ski trip. If you can earn 9% on your money, compounded monthly, how much do you need today [lump sum]?

$2496.19

Chapter 5, slide 2-36

Suppose you need $15,000 in 20 years to pay for a ski trip. If you can earn 9% on your money, compounded monthly, how much do you have to deposit monthly for 20 years?

$22.46/mo

A(n) ___________ is a series of fixed payments at regular intervals that continue forever.

perpetuity

If you are going to get infinite cash flows with a perpetuity, shouldn’t the PV be infinite?

No (Principal is never touched. Take the entire interest earned each period.)

You would like to put $500 per year aside [-ve] for 30 years and reach your goal of $250,000. What annual rate of return do you need to earn? [pv=0, why?] ]

15.70%

Chapter 5, slide 2-42

What interest rate do you need to earn to double your money in three years? [pmt=0, why?] ]

25.99%

Chapter 5, slide 2-42

You borrow $20,000 [+ve] . Your loan requires you to make 5 annual payments [-ve] of $5,000 each. What is the rate on the loan? [fv=0, why?]

7.93%

Chapter 5, slide 2-42

You borrow $30,000 for a new car at 8% interest for 3 years. What is your monthly car payment?

$940.00

Iper=8/12, N =36, FV=0

You borrow $300,000 for your new house at 7% interest for 30 years. What is your monthly house payment?

$1,995.91

i/y=7/12, n=30*12, fv=0

You want to retire in 40 years with $1 million. Assuming you can earn 10% per year, how much should you deposit at the end of each year?

PMT=? $2,259.41@pv=0, FV=1M

You want to retire in 40 years with $1 million. Assuming you can earn 10% per year, how much should you deposit at the end of each month?

FV= 1M, N=480, I/Y=10/12, PV=0-> PMT=-158.13; ->@FV=0, PV=-18,621.74, pmt= 158.13

You have $1,000 to invest now. How long will it take to achieve your goal of $1,800 if you earn 8%?

7.64 years

Mathematically:

FV/PV = (1 + i)n

Take 1n of both sides

N=ln(FV/PV)/ln(1+i)

You can set aside $500 per year at 12%, how long until you obtain $100,000?

28.40 years

Mathematically:

FV/PV = (1 + i)n

Take 1n of both sides

N=ln(FV/PV)/ln(1+i)

You borrow $15,000 from your cousin at 7%. He says you can pay him back $1,200 per year. How long will it take to pay off the loan?

30.73 years

pv=+15000, pmt=-1200, fv=0

Mathematically:

FV/PV = (1 + i)n

Take 1n of both sides

N=ln(FV/PV)/ln(1+i)

Suppose you can take a penny and double your money every day for 30 days. What will you be worth?

Iper=100%, n=30, pv=-.01, pmt=0,

Fv = $10,737,418.24

Suppose you plan to retire in 40 years and must choose between two options. Both options earn 11% per year. Which makes the most money (and how much)

1. Make 10 annual payments of $500 each beginning in one year and then make no more payments. You let your money ride for the remaining 30 years.
2. Make no retirement contributions for the first 30 years and then make 10 annual payments of $10,000 each. The tenth payment will be made the day before your retirement starts.

1. Option 1: n=10, pmt=-500, I/y=11, pv=0, àFV (1) = $8,361= pv[2], N=30, PMT=0, FV (2) = $191,403, now for N=40, pmt=0, PV=-$2945
2. Option 2: N=10, FV = $167,220, PV= minus $2572@n=40, pmt=0

Suppose you plan to retire in 40 years and you earn 11% per year. You make 10 annual payments beginning in one year and then make no more payments. You let your money ride for the remaining 30 years.

What would your annual payments need to be so you could retire with $1 million?

Work backwards!

Need $43,682.82 after 10 years {FV2=1M, I/Y=11, N=30, PMT2=0 -> PV2=? = FV1

Now, N=10, PV1=0, FV1 = 43,682.82 , PMT1=?Annuity payment: $2,612.29

For a $100,000 mortgage, @ 10% annual rate

with 30 equal annual payments.

What is the effective interest if there is a 2% [2 points]

loan origination fee, processing expenses etc.?

Calculate PMT=-10,608, [fv=0, n=30, pv=100,000]

Now enter pv=98,000, CPT, i/y= 10.24%, [because PMT remains same]

Now enter pv=-2,000,i/y=10, fv=0, CPT PMT= 212

FV of 212 @10% over 30 yrs = $34,898

Find the FV and PV of a 3% sales load and $1500 flat annual fee on a $100,000 initial investment over 10 years assuming a 10% annual return. See yahoo screener.

pv=-3000, pmt=-1500, i/y=10, n=10, FV=$31,687

With PMT=0, this is equivalent to PV =-12,217

An annuity whose payments occur at the end of each period is called:

1. an opportunity cost annuity.
2. an ordinary annuity.
3. an annuity due.
4. an outflow annuity.

B

If you deposit $12,000 per year for 16 years (each deposit is made at the beginning of each year) in an account that pays an annual interest rate of 15%, what will your account be worth at the end of 16 years?

1. $82,168.44
2. $71,450.82
3. $768,901.12
4. $668,609.67

?

Slide 2-53

_________ is he amount of annual interest income provided by the bond. Detailed on bond.

Coupon

_________ is the chance that issuer of bond will fail to make scheduled payment

Default risk

What would happen to the value of a very safe bond if market interest rates increase?

It would drop.

Ratings only reflect default risk, not interest rate risk and other risks.

_______ bonds: Issued with no (or a low) coupon rate and sold at a deep discount from par

Zero (or low) coupon

________ Bonds: Rated Ba or lower and often used to finance mergers and takeovers; high risk bonds with high yields

Junk

_______ bonds: Can be redeemed at par at the holder ’ s option at specific dates or if the firm takes specific actions

Putable

A $1,000 par value bond quoted at 96 has a price of _____

$960

A $1,000 par value bond quoted at 102.5 has a price of ______

$1,025

What is the value of a 10-year, 10% annual coupon bond, if r_d = 10%?

$1,000

Chapter 7, slide 7-22 and 7-23

There is a 10-year, 10% annual coupon bond, with r_d = 10%? Suppose you just bought this bond this morning for $1,000 when the market rate was 10%.

1. What will happen to the price of the bond if market interest rates increase to 12%?
2. What will the new price be?

1. It will drop because investors could earn higher rates elsewhere, so price of bond must be reduced as compensation.
2. $887

Assume you bought a 10-year, $1,000 par bond with $100 annual coupon payments this morning for $1,000 when market rates were 10%.

1. What will happen to the market price of the bond if market interest rates decrease to 8%?
2. What will the new price be?

1. It will increase
2. $1,134

The shorter the amount of time until maturity, the ______(more/less) responsive a bond's market value is to changes in required return

less

Suppose you have two bonds. Both bonds have $1,000 par values and pay 10% annual coupons, but one bond has 1 year remaining until maturity and the other has 10 years. If the yield curve is flat and the market interest rate for both bonds is 10%, what will the bonds sell for?

$1,000 each

Which has more interest rate risk, long-term or short-term bonds?

All things equal, long-term bonds are more sensitive to interest rate changes than short-term bonds. For an equal interest rate change, l-t bond prices will change considerably more than short-term prices.

If you think interest rates will be dropping, would you rather be holding long-term or short-term bonds?

long-term

Bond prices and interest rates are ______ (directly/inversely) related

inversely

A bond that sells for less than par is known as a ________.

discount bond

A bond will sell at a discount whenever the coupon rate is _______ (greater/less) than market rate.

less than

A bond that sells for more than par is known as a premium bond and its coupon rate is ______ (greater/less) than market rate.

greater

Assume you just bought a 5-year, $1,000 par bond with $100 annual coupon payments this morning when market rates were 8% for $1,079.85.

1. If market conditions remain unchanged, what will the value of the bond be in one year?
2. What will the value of the bond be in three years?
3. What will be the approximate value of the bond the day before it matures?

(premium bond – why? Because coupon rate =10%)

1. $1,066.24 (4 yrs to maturity ->n=5-1=4, i/y=8,pmt=100,fv=1000)
2. $1,035.67 (2 yrs to maturity ->n=5-3=2)
3. $1,000

As maturity approaches, bond values approach ______.

par

As a bond approaches maturity, its value will approach par, regardless of whether it is selling at a premium or a discount

Discount bonds will ______ (increase/decrease) in value as maturity approaches

increase

Premium bonds will ______ (increase/decrease) in value as maturity approaches.

decrease

_________ risk is the chance that cash flows have to be reinvested at an interest rate lower than what was initially being yielded.

Reinvestment

Which has more reinvestment risk, long-term or short-term bonds?

Short-term -> principal handed back

Suppose you have a 20-year investment horizon:

1. What do you do every year if you put your money in a series of one year bonds?
2. What do you do every year if you buy a 20-year bond?

1. If you buy 1-year bonds, every year of the 20 year period you have to reinvest principal and interest.
2. If you bought a 20-year bond instead, only coupon payments would need to be reinvested.

Although 1 year bonds have little interest rate risk, they have more reinvestment risk

True or False: All 10-year bonds have the same price and reinvestment rate risk.

False! Depends on coupon level -> Low coupon bonds have less reinvestment rate risk but more price risk than high coupon bonds.

Long-term bonds: _____ (high/low) interest rate risk, ______ (high/low) reinvestment rate risk – for principal

High interest rate risk, low reinvestment rate risk

(however the coupon payments are still exposed to the prevailing interest rates).

Short-term bonds: _____ (high/low) interest rate risk, ______ (high/low) reinvestment rate risk – for principal

Low interest rate risk, high reinvestment rate risk

1. If B0 > face value, then K_d _____ (greater/less) than coupon rate
2. If B0 < face value, then K_d _______ (greater/less) than coupon rate

1. less
2. greater

Chapter 7, slide 7-37

_______ is the rate of return investors expect to earn if they buy a bond at a specific price and hold it until maturity

Yield To Maturity (YTM)

What is the YTM on a 10-year, 9% annual coupon, $1,000 par value bond, selling for $887?

10.97%

This bond sells at a discount, because YTM > coupon rate.

Chapter 7, slide 7-38, 7-39

Find YTM, if the bond price was $1,134.20.

7.08%

This bond sells at a premium, because YTM < coupon rate.

Chapter 7, slide 7-40

Find the current yield and the capital gains yield for a 10-year, 9% annual coupon bond that sells for $887, and has a face value of $1,000. If market conditions stay the same, what will the price of our bond be in one year?

CY = 10.15%

CGY = 0.76%

Chapter 7, slide 7-44, 7-45

What is the value of a 10-year, 10% semiannual coupon bond, if kd = 13%?

? $834.72

Chapter 7, Slide 7-48

1. Would you prefer to buy a 10-year, 10% annual coupon bond or a 10-year, 10% semiannual coupon bond, all else equal?
2. If the proper price for this semiannual bond is $1,000, what would be the proper price for the annual coupon bond [same EAR]?

1. Semiannual bond (10.25% > 10%)
2. ??$984.80

Chapter 7, Slide 7-49 and 7-50

Is a AAA rating a protection from a drop in value of bond?
***ON EXAM!

What would happen to the value of a very safe bond if market interest rates increase?
It would drop.
Ratings only reflect default risk, not interest rate risk and other risks