Multiplication Postulate

If equal quantities are multiplied by equal quantities then the products are equal
If A = B, then A x C = B x C.

Division Postulate

If equal quantities are divided by equal nonzero quantities then the quotions are equal
If A = B, then A / C = B / C.

Substitution Postulate

A quantity and its equal(s) are interchangeable in an expression. If abc=def is given, and ab+de=abc, then ab+de=def would be true.

Partition Postulate

The whole is equal to the sum of its parts.
Also: Betweeness of points AB + BC AC
Angle Addition Postulate: m<ABC + m<CBD = m<ABD

Construction Straight line

Two Points determine a straight line

Construction Perpendicular

From a given point one and only one perpendicular can be drawn to the line.

Right Angles

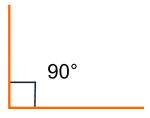All Right angles are congruent. All right angles = 90 degrees. Formed by 2 lines perprndicular to each other

Straight Angles

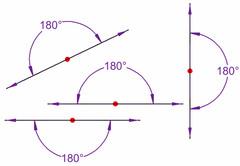An angle whose sides lie in opposite directions from the vertex in the same straight line and which equals two right angles

Congruent Supplements

If two angles are supplements of the same angle (or of congruent angles), then the two angles are congruent
m<A + m<B = 180 Degrees and m<A + m<C = 180 Degrees Then m<B + m<C = 180 Degrees and <B = <C

Congruent Compliments

If two angles are compliments of the same angle (or of congruent angles), then the two angles are congruent. Compliments of the same angle or congruent angles are congruent
IF m<A + m<B = 90 Drgrees and m<B + m<C = 90 Degrees Then m<B + m<C = 90 Degrees<B = <C

Linear Pair

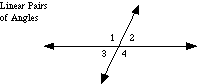If two angles form a linear pair,then they are supplementary (m < 1 + m< 2 = 180 Degrees). Two angles that are adjacent (share a leg) and supplementary (add up to 180°)

Vertical Angles

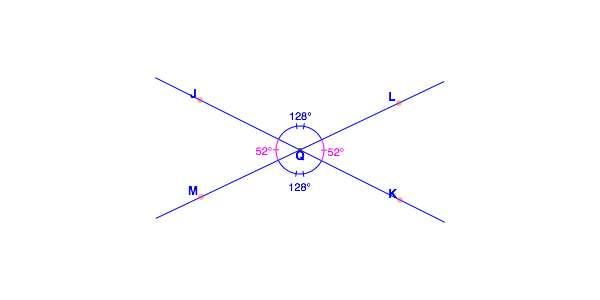Vertical angles are on opposite sides of the X formed when two lines intersect Vertical Angles are congruent.They are congruent Vertical angles are always congruent, or of equal measure. Both pairs of vertical angles (four angles altogether) always sum to a full angle (360°).

Triangle Sum

The sum of the interior angles of a triagle is 180 Degrees

Exterior Angle

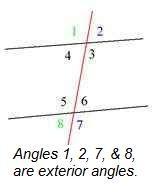The measure of an exterior angle of a triangle is equal to the sum of the measures of the two non-adjacent interior angles. The measure of an exterior angle of a triangle is greater than either non-adjacent interior angle

Base Angle Theorem
(Isosceles Triangle)

If two sides of a triangle are congruent, the angles opposite are congruent

Corresponding Angles Converse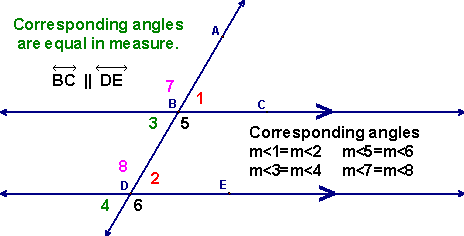

If two parallel lines are cut by a transversal, and the corresponding angles are congruent the lines are parallel

Corresponding Angles

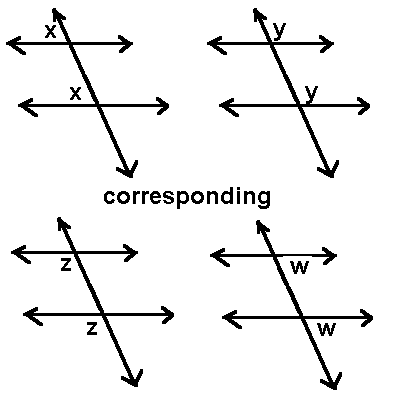If two lines are cut by a transversal, then the pairs of corresponding angles are congruent

Alternate Interior Angles

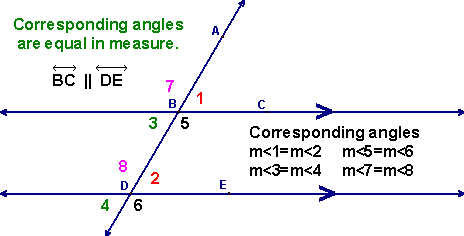If two parallel lines are cut by a transversal, then the alternate interior angles are congruent.
<5 = <6

Alternate Exterior Angles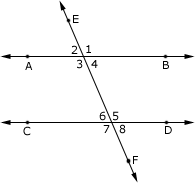

Formed when two lines are cut by another line (transversal), the pairs of angles formed outside the two lines and on the opposite of the transversal.
If two parallel lines are cut by a transversal, then the alternate exterior angles are congruent.
AB || CD and EF is the transversal cutting the parallel lines. So, ∠2 and ∠8;and ∠1 and ∠7 are the pairs of alternate exterior angles in the figure shown.

Interiors on Same Side Angles

If two parallel lines are cut by a transversal,the interior angles on the same side of the transversal are supplemetary.
<4 and < 5 are Interior Same side angles so are <3 and <6

Alternate Interior Angles Converse

If two lines are cut by a transversal and the alternate interior angles are congruent then the lines are parallel
Transversal EFGH intersects lines AB and CD such that a pair of alternate E are equal.
Since the corresponding angles of the lines AB and CD are equal, the lines are parallel.

Alternate Exterior Angles Converse

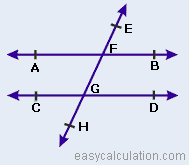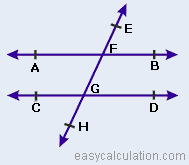If two lines are cut by a transversal and the alternate exterior angles are congruent then the lines are parallel or
If a transversal intersects two lines in such a way that a pair of alternate interior angles are equal, then the two lines are parallel.

Interiors on Same Side Converse

If two lines are cut by a transversal and the interior angles on the same side of the transversal are supplementary then the lines are parallelor If two lines and a transversal form same-side interior angles that are supplementary, then the lines are parallel.

Acute Angle

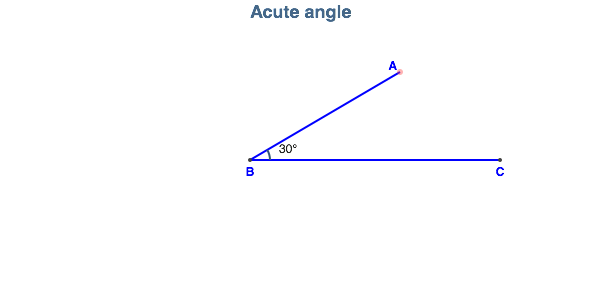Any angle whose measure is less than 90 degrees. Does not include 0 or 90 Degrees

Adjacent Angles

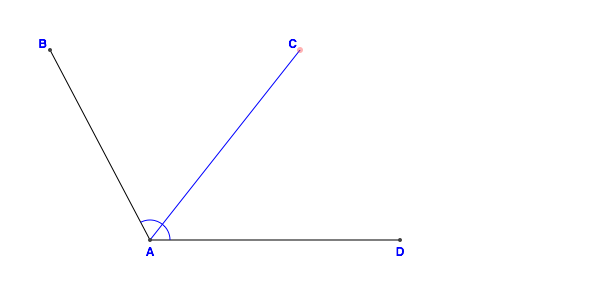Angles that share a vertex and that have a side in common.

Midpoint

A point that divides a segment into two congruent segments. The point on that line segment that divides the segment two congruent segments.

Perpendicular

Forming right angles. Right angles measure 90 degrees

Postulate

A geometic statement assumed to be true without proof

Same-Sided Exterior Angles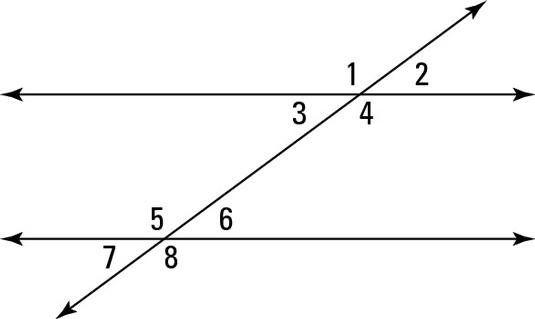

Angles on the same side of the transversal, and they’re outside the parallel lines. <7 and <1 also <8 and <2

Two same-side exterior angles are supplementary.
m<7 + m<1 = 180 degrees and m<2 + m<8 = 180 Degrees

Same-Sided Interior Angles

If two parallel lines are cut by a transversal, the interior angles on the same side of the transversal are supplementary.
If two lines are cut by a transversal and the interior angles on the same side of the transversal are supplementary, the lines are parallel.

Transversal

A line that crosses two parallel lines

Vertical Angles

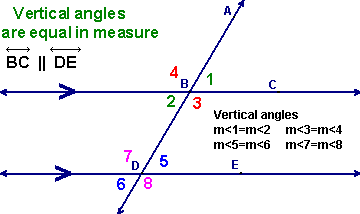Congruent anglea formed by two intersectin lines that make an X; the vertical angles are on opposite sides of the X.

Segment Addition Postulate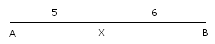

In the diagram we have AX = 5 and XB = 6. AB = 5 + 6 = 11.

Subtraction Property of Equality

States that when both sides of an equation have the same number subtracted from them, the remaining expressions are still equal.

If 12x = 24x/2, then 12x - 7 = 24x/2 - 7.

If a = b, then a - c = b - c.

Symmetric Property of Equality

If we have an equation like
3x - 5 = y
we can rewrite that as
y = 3x - 5
and it is still true.
If a number is equal to a second number, then the second number is also equal to the first.
if 13 – 5 = 8 then 8 = 13 – 5.
If 4•5 = 20 then 20 = 4•5.

Substitution Poperty of Eqrality

If I know that two variables both refer
to the same number (that's what "equal" means), then anything I say about one of them is also true of the other
If a = b, then b can replace a in any equation without changing the truth value of the equation. For example:
Let a = b.
Let d = a + 2.
Then d = b + 2.

Converse Conditional Statement

This form of a conditional statement is obtained by interchanging the hypothesis and conclusion. If it is the first of the month then the rent is due becomes If the rent is due then it is the first of the month

Inverse Conditional Statement

This form of a conditional statement is obtained by negating the hypothesis and negating the conclusion. If it is the first of the month then the rent is due becomes If it is not the first of the month then the rent is not due

Contrapositive Conditional Statement

This form of a conditional statement is obtained by interchanging and negating the hypothesis and conclusion. If it is the first of the month then the rent is due becomes If the rent is not due then it is not the first of the month

Syllogism

An instance of a form of reasoning in which a conclusion is drawn (whether validly or not) from two given or assumed propositions (premises), each of which shares a term with the conclusion, and shares a common or middle term not present in the conclusion (e.g., all dogs are animals; all animals have four legs; therefore all dogs have four legs ).
If q, then r. If p then q is true and if q then r is true then p then r is also true.

Venn Diagrams

a diagram that shows all possible logical relations between a finite collection of sets.The diagram shows and or or nor relationships

Hypothesis

The "If" part of a statement. A statement that might be true, which can then be tested

Conclusion

The "then" part of a conditional statement.

Conditional Statement

Name for an If...Then statementA compound statement formed by joining two statements with "if" and "then"

Statement

A declarative statement which is either true or false, but never both

Negation

Sometimes in mathematics it's important to determine what the opposite of a given mathematical statement. If a statement is true, then its opposite is false (and if a statement is false, then its opposite is true).
usually be formed by placing the word "not" into the original statement. The negation will always have the opposite truth value of the original statement.
Under negation, what was TRUE, will become FALSE -
or - what was FALSE, will become TRUE.

Conjunction A and B

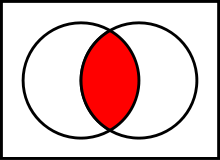A compound statement resulting from the joining of two statements using an AND. Both statements must be true for the conjunction to be true.
n logic and mathematics, a two-place logical operator and, also known as logical conjunction,[1] results in true if both of its operands are true, otherwise the value of false

Disjunction

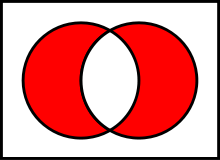A compound statement resulting from the joining of two statements using OR.If both statements are false Then the compound is false.Logical OR is also known as logical disjunction. Disjunction literally means "a state of being disjoined". Logical disjunction holds when at least one of the given conditions is true. It is a binary operator which requires at least two operands for its application.

Theorem

A statement of a mathematical fact that can be proved

The law of Detachment

A form of deductive reasoning that is used to draw conclusions from true conditional statements. If p then q is true then p is true and q is true.
Syllogism works with the statments "P implies Q" and "Q implies R" (notice Q is mentioned twice). If both those statements are true, then the statement "P implies R" is true.

Transitive property of equality:

if a number is equal to a second number, and the second number is equal to a third, then the first number and the third number are also equal.
If 3 + 7 = 10 and 10 = 4 + 6, then 3 + 7 = 4 + 6.
If 22 / 11 = 2 and 2 = 18 / 9, then 22 / 11 = 18 / 9.

Alternate Exterior Angles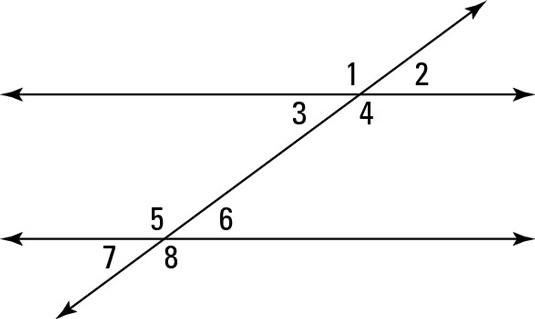

Defined as two exterior angles on opposite sides of a transversal which lie on different parallel lines.
ngles 1 and 8 (and angles 2 and 7) are called alternate exterior angles. They’re on opposite sides of the transversal, and they’re outside the parallel lines.

Alternate Interior Angles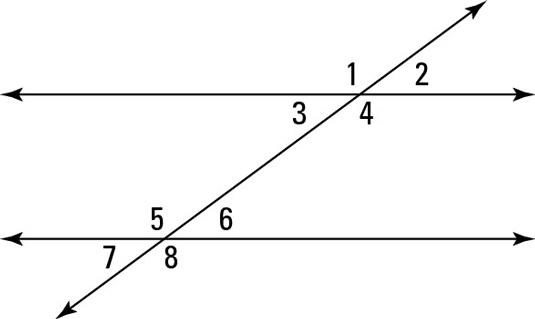

two interior angles which lie on different parallel lines and on opposite sides of a transversal.he pair of angles 3 and 6 (as well as 4 and 5) are alternate interior angles. These angle pairs are on opposite (alternate) sides of the transversal and are in between (in the interior of) the parallel lines.

Consecutive Interior Angles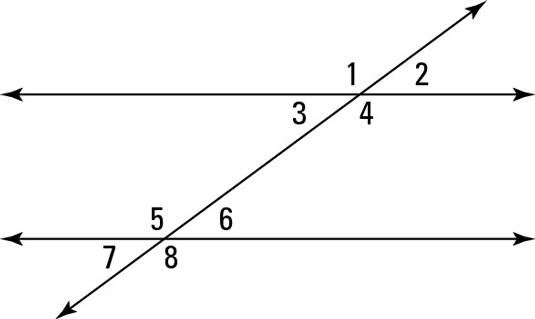

In the figure above, angles 4 and 6 are consecutive interior angles. So are angles 3 and 5. Consecutive interior angles are supplementary. The pairs of angles on one side of the transversal but inside the two lines are called Consecutive Interior Angles.

Congruent

Exactly equal in size and shape. Congruent sides or segments have the exact same length. Congruent angles have the exact same measure. For any set of congruent geometric figures, corresponding sides, angles, faces, etc. are congruent.

Concurrent

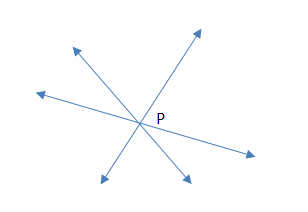Lines or curves that all intersect at a single point.

Coincident

Identical, one superimposed on the other. That is, two or more geometric figures that share all points. For example, two coincident lines would look like one line since one is on top of the other.

Contrapositive

Switching the hypothesis and conclusion of a conditional statement and negating both. For example, the contrapositive of "If it is raining then the grass is wet" is "If the grass is not wet then it is not raining."

Note: As in the example, the contrapositive of any true proposition is also true.

Converse

Switching the hypothesis and conclusion of a conditional statement. For example, the converse of "If it is raining then the grass is wet" is "If the grass is wet then it is raining."

Note: As in the example, a proposition may be true but have a false converse.

Inverse of a Conditional

Negating both the hypothesis and conclusion of a conditional statement. For example, the inverse of "If it is raining then the grass is wet" is "If it is not raining then the grass is not wet".

Note: As in the example, a proposition may be true but its inverse may be false.

Iff
if and only if
Biconditional

A way of writing two conditionals at once: both a conditional and its converse.
For example, the statement "A triangle is equilateral iff its angles all measure 60°" means both "If a triangle is equilateral then its angles all measure 60°" and "If all the angles of a triangle measure 60° then the triangle is equilateral".

Corresponding

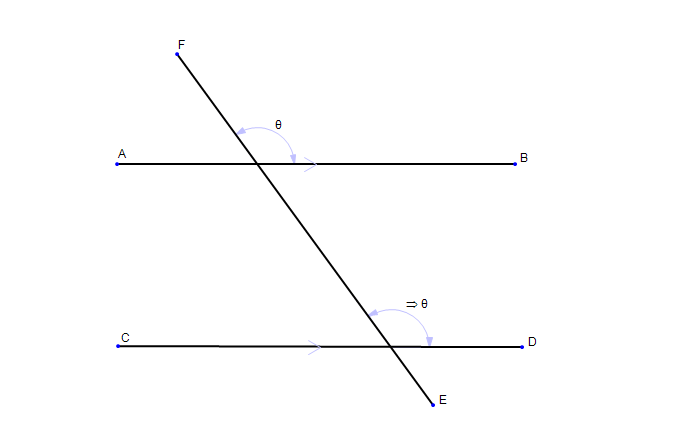Two features that are situated the same way in different objects.

Linear Pair of Angles

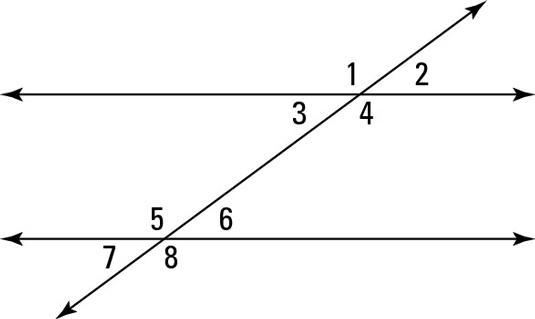A pair of adjacent angles formed by intersecting lines. Angles 1 and 2 below are a linear pair. So are angles 2 and 4, angles 3 and 4, and angles 1 and 3. Linear pairs of angles are supplementary.

Parallel Lines

Two distinct coplanar lines that do not intersect. Note: Parallel lines have the same slope.

Straight Angle

A 180° angle.

Transversal

A line that cuts across a set of lines or the sides of a plane figure. Transversals often cut across parallel lines.

Interior Angle

An angle on the interior of a plane figure.

Examples: The angles labeled 1, 2, 3, 4, and 5 in the pentagon are all interior angles. Angles 3, 4, 5, and 6 in the second example below are all interior angles as well (parallel lines cut by a transversal).
Note: The sum of the interior angles of an n-gon is given by the formula (n – 2)·180°. For a triangle this sum is 180°, a quadrilateral 360°, a pentagon 540°, etc.

Properties of Angle Congruence

Angle congruence is reflexive, symmetric, and transitive. Here are some examples.
REFLEXIVE: For any angle <A = <A

TRANSITIVE: If <A = <B and < B = <C then <A = <C

SYMMETRIC: If <A = <B then <B = <A