Instructions for Side by Side Printing
- Print the notecards
- Fold each page in half along the solid vertical line
- Cut out the notecards by cutting along each horizontal dotted line
- Optional: Glue, tape or staple the ends of each notecard together
CHAPTER 8B Problem Solving
front 1 8B.2 In what ways does the quantum mechanical description of a harmonic oscillator merge with its classical description at high quantum numbers? | back 1 The correspondence principle (mentioned in Topic 8A.2(b)) states that
in the limit of very large quantum numbers quantum mechanics merges
with classical mechanics. The harmonic oscillator provides an example.
A classical harmonic oscillator’s range of motion is restricted by
classical turning points, which are determined by the oscillator’s
total energy; that energy can take on any real positive value. By
contrast, a quantum harmonic oscillator can tunnel past classical
turning points into the classically forbidden region with
a |
front 2 8B.1(b) Calculate the zero-point energy of a harmonic oscillator consisting of a particle of mass 5.16 × 10−26 kg and force constant 285 N m−1. | back 2 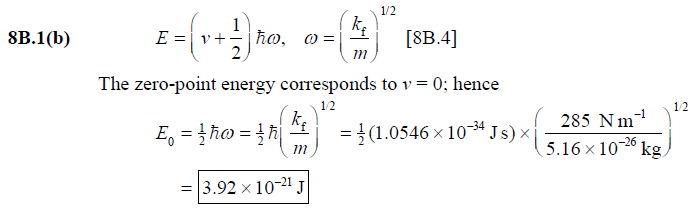 |
front 3 8B.2(b) For a certain harmonic oscillator of effective mass 2.88 ×
10−25 kg, the difference in adjacent energy levels is 3.17 zJ.
Calculate the force constant of | back 3 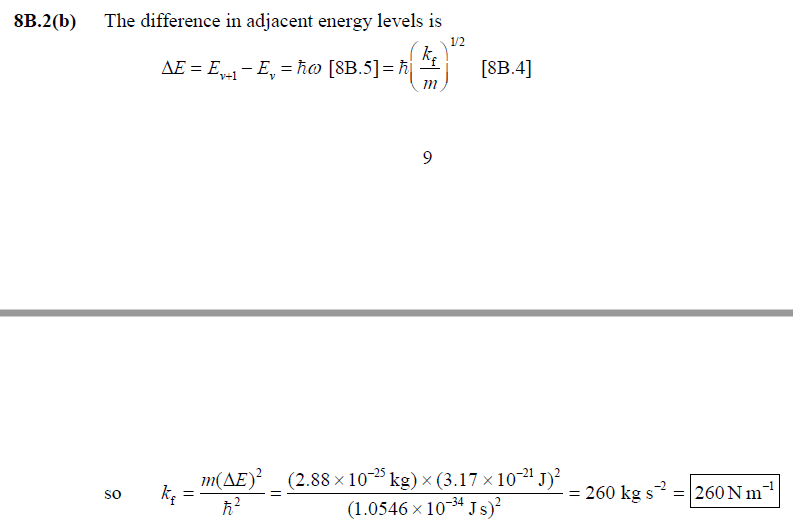 |
front 4  8B.6(b) | back 4 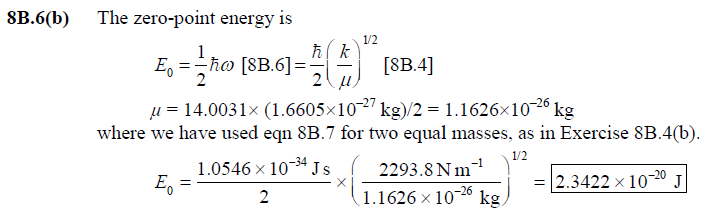 |
front 5 8B.7(b) Locate the nodes of the harmonic oscillator wavefunction with v = 5. | back 5  |
front 6 8B.8(b) What are the most probable displacements of a harmonic oscillator with v = 3? | back 6  |