Ratio Test:
When does it converge & diverge & is inconclusive.

if the lim n-> ∞ < 1 then the series converges
if the lim n-> ∞ < 1 then the series Diverges
if the lim n-> ∞ == 1 then the series is inconclusive
P - Series:
When does a series converge, and diverge.
The Series converges if P> 1, diverges if P <= 1.
Divergence Test / (nth term divergence test):
When does it converge & diverge & is inconclusive.

of the lim n-> 0, then the test is inconclusive.
Direct Comparison Test:
When does a series converge, and diverge.

- If 0≤an≤bn (bn converges then an also converges)
- If an≥bn≥0 (if bn diverges then an also diverges)
Limit Comparison Test:
What is the formula for the test?
What does L have to be to converge?
What does L have to be to diverge?

If L is a finite positive number (0 < L < ∞)
Both series (an) and (bn) either converge or diverge)
If L = 0 and Bn converges
An also converges
if L = ∞ and Bn Diverges
then An also diverges
Alternating Series Test:
When does it converge, and diverge?
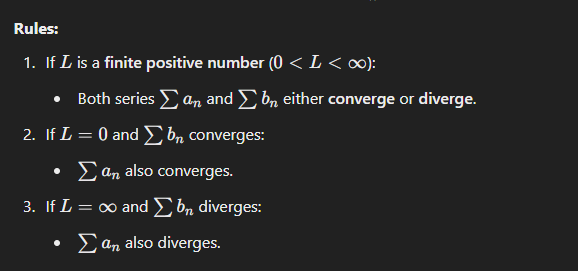
When Lim n->oo an = 0
Geometric Series:
What is the series look like? when does it converge and diverge?

If |R| >= 1 then it diverges, |R| < Converges.
Integral Test:
What does f(x) need to be to converge.

- Continuous,
- Positive,
- Decreasing for x≥1 then the series and the corresponding improper integral either both converge or both diverge.